船用调节阀有两种基本的流量特性:
线性流量特性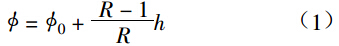
等百分比流量特性 Ф=Ф0Rh (2)
式中:Ф 为对应某开度是的流量系数;R 为可调比;h 为相对开度;Ф0 为 h=0 是的流量系数。
按照传统的解释,可调比 R 是指所能控制最大流量的比值,即
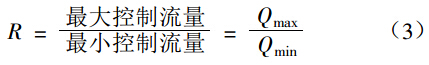
在设计调节阀时,需先设定一个 R 值,然后计算各开度下的流量系数 Ф,以此作为设计阀芯曲线和套简窗口的依据。国内调节阀行业的两次统一设计,都是在设定 R=30 前提下,计算出了各开度对应的流量系数理论值(见表 1)。
| 流量特性 | Ф0 | 各相对开度 Ф 值 | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
| 线性 | 3.33 | 13.00 | 22.67 | 32.33 | 42.00 | 51.67 | 61.33 | 71.00 | 80.67 | 90.33 | 100.00 |
| 等百分比 | 3.33 | 4.68 | 6.58 | 9.25 | 12.99 | 18.26 | 25.65 | 36.05 | 50.65 | 71.17 | 100.00 |
从应用角度,希望调节阀的放大倍数 KD 大一些,而 KD 与可调节比 R 有关,
线性特性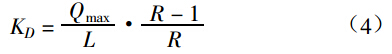
等百分比特性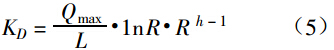
式中:L 为全行程开度。可以看出,增大 KD,应提高 R 值,因此,制造厂都将可调比大于某一数值作为一项性能指标予以标明。但是调节阀 R 值越大,设计制造难度越大。对单、双座调节阀,若 R 值过大,阀芯制造时会在 90%~100% 开度范围内产生根切现象;对套筒调节阀,若 R 值太大,在 90%~100% 开度范围内会因窗口尺寸过宽而无法制造。这些都限制了 R 值的提高。
制造厂是在 R=30 前提下设计制造出调节阀产品,但对调节阀产品实际 R 值是多大、它与 R=30 的偏差等问题,目前尚未引起人们的重视。由于,设计人员对 R 值的认识仅局限在 Qmax 和 Qmin 的比上,而 Qmin 只是个理论上存在的数值,无法进行测量,因此认为实际可调比也是无法计算的。在目前见到的有关调节阀的资料中,尚未看到这方面的论述。国内外调节阀的 标准中,也未提出对 R 值的测量、计算和考核办法。这是由于对可调比概念的片面理解所造成的,现在有必要从可调比与流量系数的关系入手作进一步探讨与研究。
1、可比阀与流量特性曲线的关系
从流量系数的计算公式可以看出,R 值取决于,但它决定了任意一个相对行程时的流量系数值。因此,无论从调节阀的设计、制造和应用角度讲,这一点都具有很重要的实际意义。因为,任何调节阀都不可能使用在它的最小开度,也就是不会用其 Qmin 来工作,大量的使用场合是在某一开度(一般在全行程的 20%~80%)上对流量进行控制。此时,调节阀的流量系数大小决定了调节阀的工作开度,流量系数相对于行程的变化量决定了调节阀的放大倍数,这些均与 R 值有关。因此,不能简单地从 Qmax 和 Qmin 的比去理解 R 值,而应当把 R 值看作是整个流量特性曲线的一个特征参数。
分析式(1)、式(2)与式(3)、式(4)可以看出,R 值变化对线性流量特性影响不大,特别在 R>1 时,Ф 与 KD 均与 R 值无关;对等百分比特性影响则较大,因此本文讨论值对流量系数的影响仅限于等百分比特性。
当 R 值作为流量特性曲线的一个特征参数时,可以设想将全行程的流量特性曲线看成由几个不同 R值决定的几段流量特性曲线组合而成。在 0~80% 开度时,R 值取大一些,使调节阀在工作行程范围内有足够的 R 值,也就是有足够的放大倍数。在 80%~100% 开度范围,R 值取小一些,使调节阀制造过程中,阀芯曲线和套筒开窗都容易实现。提高工作开度下的 R值,也可以作为在调节阀设计中探索提高流通能力的一个途径。分段取不同的 R 值这一思想,已从 IEC534—2—4(草案)和国外一些调节阀流量系数表中体现出来,这时可调比的含义已经不再是 Qmax 和 Qmin 之比了,它应当作为流量特性曲线的一个特征参数被认识、被研究。
2 R 值计算方法
调节阀实际可调比 R 值是可以计算出来的,根据公式(2)可推导出
lnФ=lnФ0+hlnR (6)
在 lnФ—h 坐标系中,等百分比流量特性曲线是一直线,R 值实际上决定了该直线的斜率。实际测量一台调节阀的流量特性,可以得到若干组(Ф,h)数据,由于制造和测量误差,这些测量值在 lnФ—h 坐标系中呈近似直线分布,并认为这条近似直线就是这台调节阀的实际流量特性曲线。要得到这样一条直线,并使其最接近坐标系中的这些点,建议用最小二乘法求解。
在测量一台调节阀于不同开度时的流量系数时,可以得到相对行程和流量系数的 K 组数据,代入公式(6)得到方程组
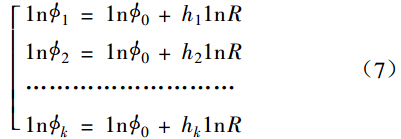
式中:Ф0,R 为这台调节阀的实际值,可从方程组(7)中用最小二乘法求其近似值:
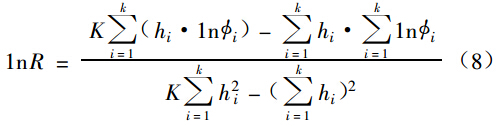
一般情况下取 10 个开度进行测量,即 hi 分别去 0.1,0.2,0.3,…,1.0。此时有 K=10,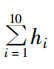 =5.5;
=5.5;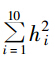 =3.85,代入式(8)则有
=3.85,代入式(8)则有
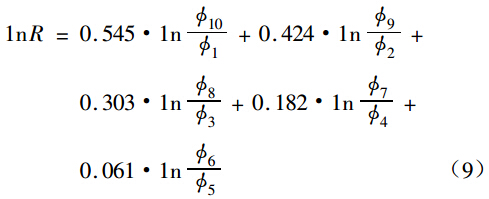
将测量所得流量系数 Фi 代入公式(9),即可解出该台调节阀的实际可调比 R 值。若将表 1 中等百分比流量系数的理论值代入公式(9),即可反算出 R=30。按式(9)解出的是全行程的可调比,为了准确了解调节阀在工作段的可调比,hi 可分别取 0.2,0.3,…,0.8,即 k=7,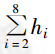 =3.5,
=3.5,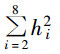 =2.03,则有
=2.03,则有

代入 20%~80% 开度时的各流量系数,可以得到该段流量特性的 R 值。同样,将表 1 中理论值数据代入式(10),也可反算出 R=30。由于式(9)、式(10)中 Ф 值都是以比值形式出现,无论用绝对流量系数或相对流量系数计算其结果都是相等的。因此,用来计算 R 值是很方便的。同样,当需要计算任意段流量特性曲线的 值时,都可以推出相应的计算公式。
3 国内外一些调节阀 R 值的比较
依据式(9)用国内统一设计的双座调节阀和联合设计的套筒调节阀,以及 Fisher 公司的 ED 型套筒阀的流量系数计算相应的 R 值,其结果见表 2~表 4。
从表中可以看出,尽管双座调节阀和套筒调节阀在设计时预先设定 R=30,但实际生产的各种规格的调节阀其 R 值是不相同的。
| 公称通径 DN×dN | 各相对开度 Ф 值 | 可调比 R | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
| 25 | 2.65 | 4.57 | 7.84 | 12.76 | 17.96 | 25.04 | 35.00 | 49.11 | 74.53 | 103.39 | 51.5 |
| 32 | 3.09 | 6.30 | 9.90 | 13.99 | 18.90 | 24.60 | 30.10 | 42.80 | 74.40 | 100.00 | 34.6 |
| 40 | 7.44 | 10.28 | 11.52 | 13.22 | 16.88 | 21.92 | 28.82 | 52.84 | 78.92 | 92.00 | 17.4 |
| 50 | 7.68 | 11.89 | 14.90 | 18.40 | 22.90 | 29.50 | 37.80 | 53.50 | 70.40 | 98.20 | 14.6 |
| 65 | 3.95 | 7.72 | 11.36 | 15.53 | 20.20 | 26.56 | 36.51 | 50.77 | 77.53 | 99.58 | 28.9 |
| 80 | 3.34 | 7.64 | 10.49 | 14.63 | 19.85 | 28.00 | 37.75 | 50.28 | 75.49 | 97.25 | 32.4 |
| 100 | 4.70 | 7.68 | 10.32 | 14.20 | 18.81 | 27.35 | 37.02 | 52.82 | 72.39 | 97.60 | 27.1 |
| 125 | 4.14 | 6.49 | 9.47 | 12.89 | 19.37 | 27.61 | 37.34 | 51.88 | 66.66 | 103.63 | 32.3 |
| 150 | 2.55 | 5.70 | 8.50 | 12.42 | 18.17 | 25.45 | 34.98 | 48.48 | 76.74 | 96.81 | 45.7 |
| 200 | 12.20 | 16.10 | 20.10 | 25.10 | 32.00 | 46.50 | 75.80 | 100.50 | 20.0 | ||
| 公称通径 DN×dN | 各相对开度 Ф 值 | 可调比 R | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
| 25 | 4.10 | 7.90 | 12.10 | 16.50 | 20.40 | 29.60 | 42.20 | 61.00 | 81.50 | 103.00 | 30.9 |
|
40 C=16 |
2.12 | 6.06 | 10.00 | 14.31 | 18.75 | 24.75 | 34.50 | 51.06 | 73.75 | 96.88 | 45.3 |
|
60 C=25 |
6.54 | 9.12 | 11.76 | 14.84 | 20.24 | 28.16 | 38.60 | 56.00 | 78.00 | 99.20 | 21.3 |
| 50 | 3.10 | 6.45 | 9.90 | 15.05 | 22.48 | 32.50 | 46.50 | 67.50 | 90.50 | 97.75 | 45.2 |
| 65 | 3.25 | 6.83 | 10.24 | 14.63 | 20.63 | 27.46 | 40.32 | 58.73 | 86.35 | 107.94 | 41.2 |
| 80 | 4.20 | 7.67 | 11.10 | 14.97 | 21.05 | 29.70 | 40.60 | 60.50 | 80.10 | 92.60 | 29.9 |
| 100 | 3.57 | 7.37 | 11.03 | 15.21 | 21.80 | 30.39 | 44.13 | 64.90 | 82.06 | 93.23 | 34.9 |
|
125 C=250 |
3.69 | 7.00 | 10.80 | 15.24 | 21.20 | 29.80 | 41.60 | 59.60 | 87.60 | 102.80 | 36.9 |
|
125 C=370 |
3.34 | 7.14 | 10.84 | 15.19 | 21.89 | 31.62 | 45.95 | 65.41 | 82.43 | 93.24 | 37.5 |
| 200 | 3.17 | 6.90 | 10.79 | 15.66 | 22.41 | 31.90 | 42.76 | 60.34 | 81.21 | 96.03 | 37.8 |
| 300 | 3.31 | 6.92 | 10.54 | 14.54 | 20.23 | 28.62 | 43.85 | 64.23 | 82.31 | 94.08 | 38.3 |
| 公称通径 DN×dN | 各相对开度 Ф 值 | 可调比 R | |||||||||
| 0.1 | 0.2 | 0.3 | 0.4 | 0.5 | 0.6 | 0.7 | 0.8 | 0.9 | 1.0 | ||
|
1*1/4×1*5/16 |
0.783 | 1.54 | 2.20 | 2.89 | 4.21 | 5.76 | 7.83 | 10.9 | 14.1 | 17.2 | 27.4 |
| 1*1/2×1*7/8 | 1.52 | 2.63 | 3.87 | 5.41 | 7.45 | 11.2 | 17.4 | 24.5 | 30.8 | 35.8 | 36.3 |
| 2×2*5/16 | 1.66 | 2.93 | 4.66 | 6.98 | 10.8 | 16.5 | 25.4 | 37.3 | 50.7 | 59.7 | 57.6 |
| 2*1/2×2*7/8 | 3.43 | 7.13 | 10.8 | 15.1 | 22.4 | 33.7 | 49.2 | 71.1 | 89.5 | 99.4 | 41.3 |
| 3×3*7/16 | 4.32 | 7.53 | 10.9 | 17.1 | 27.2 | 43.5 | 66.0 | 97.0 | 120 | 136 | 54.2 |
| 4×4*3/8 | 5.85 | 11.6 | 18.3 | 30.2 | 49.7 | 79.7 | 125 | 171 | 205 | 224 | 64.8 |
| 6×7 | 12.9 | 25.8 | 43.3 | 67.4 | 104 | 162 | 239 | 316 | 368 | 394 | 47.1 |
| 8×8L=2 | 18.5 | 38.0 | 58.4 | 86.7 | 130 | 189 | 268 | 371 | 476 | 567 | 41.9 |
| 8×8L=3 | 27.0 | 58.1 | 105 | 188 | 307 | 478 | 605 | 695 | 761 | 818 | 43.1 |
比较表 2、表 3 这两个系列调节阀的 R 值可以看出,双座调节阀各种规格的 R 值偏差较大,套筒调节阀各种规格的 R 值偏差较小。这与两种阀设计时对流量特性采用不同误差判定标准相吻合,双座调节阀以最大流量值的 10% 作为每个行程流量值的偏差范围,而套筒阀采用国际 IEC 标准中的斜率法计算流量特性偏差的方法。显然,后一种方法较前一种方法更能保证 R 值达到设计要求,这也说明了 IEC 标准斜率法的先进性。
比较表 2、表 3、表 4 还可以看出,国产调节阀的 R 值比国外调节阀小,国内双座阀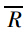 =30.5、套简阀
=30.5、套简阀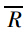 =36.2;Fisher 公司 ED 型套简阀
=36.2;Fisher 公司 ED 型套简阀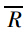 =45.9。
=45.9。
再按式(10)计算国内套简阀和 Fisher 公司 ED 型套简阀在工作行程段(h=0.2~0.8)时的 R 值,并与全行程时的 R 值相比较,结果见表 5 与表 6。可以看出,国产套简阀工作行程段的 R 值和全行程 R 值接近,无显著改变,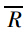 =34.2,而 Fisher 公司套简阀在工作行程段的 R 值明显高于全行程的 R 值,
=34.2,而 Fisher 公司套简阀在工作行程段的 R 值明显高于全行程的 R 值,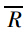 =60.5。
=60.5。
提高工作行程段的 R 值,其优越性在于它能更好地满足自控系统的需要,还能提高 80% 开度时的流量系数值,从而使全开时阀的流通能力有较显著的提高。通过对 R 值的分析比较,说明了国内外调节阀在设计水平上存在一定的差距。
| 套筒阀行程段 | 套筒阀各规格 R 值 | R 平均 | ||||||||||
| 20 |
40 C=16 |
40 C=25 |
50 | 65 | 80 | 100 |
125 C=250 |
125 C=370 |
200 | 300 | ||
| 全行程 | 30.9 | 45.3 | 21.3 | 45.2 | 41.2 | 29.9 | 34.9 | 36.9 | 37.5 | 37.8 | 38.3 | 36.2 |
| h=0.2~0.8 | 26.9 | 28.9 | 20.5 | 49.2 | 33.4 | 29.5 | 35.4 | 33.0 | 39.2 | 35.2 | 38.4 | 34.2 |
| 套筒阀行程段 | 套筒阀各规格 R 值 | R 平均 | ||||||||
| 1*1/4×1*5/1 | 1*1/2×1*7/8 | 2×2*5/16 | 2*1/2×2*7/8 | 3×3*7/16 | 4×4*3/8 | 6×7 | 8×8L=2 | 8×8L=3 | ||
| 全行程 | 27.4 | 35.3 | 57.6 | 41.3 | 54.2 | 64.8 | 67.1 | 41.9 | 43.1 | 45.9 |
| h=0.2~0.8 | 25.8 | 41.5 | 69.7 | 46.2 | 78.1 | 99.7 | 69.0 | 45.0 | 69.7 | 60.5 |
4、对 IEC 534—2—4(草案)的理解
IEC 534—2—4(草案)第 3.3 款对等百分比流量特性做了如下规定:
“在 h=0.2 和 h=0.8 之间,任意两个相邻流量系数发表值的对数之间的差值应在 0.13 和 0.2 范围内”。“低于 h=0.2 这两个值相应为 0.13 和 0.25;高于 h=0.8,此值应相应为 0.03 和 0.2”。
这里作为流量特性偏差范围的选取,应当看作是按 R 值的变化范围决定的,试计算
R=20,0.1×logR=0.13
R=100,0.1×logR=0.20
R=300,0.1×logR=0.25
R=2,0.1×logR=0.03
也就是说,流量特性偏差实际上是分段限制 R 值的变化范围,即
h=0.2~0.8,R=20~80;
h=0.8~1.0,R=2~100;
h=0~0.2,R=20~300;
IEC 的这一规定正是体现了将 R 值作为流量特性曲线的一个特征参数,并实现了在全行程范围内可以取不同 R 值这一设计思想。而国标 GB 4213—84《气动调节阀通用技术条件》在这个问题上是和 IEC 标准存在一定差异的。深入讨论 R 值及流量系数的关系,无论对设计、制造、应用调节阀都有一定的意义,对加强调节阀的基础理论研究,提高我国调节阀设计制造水平,都是十分必要的。




